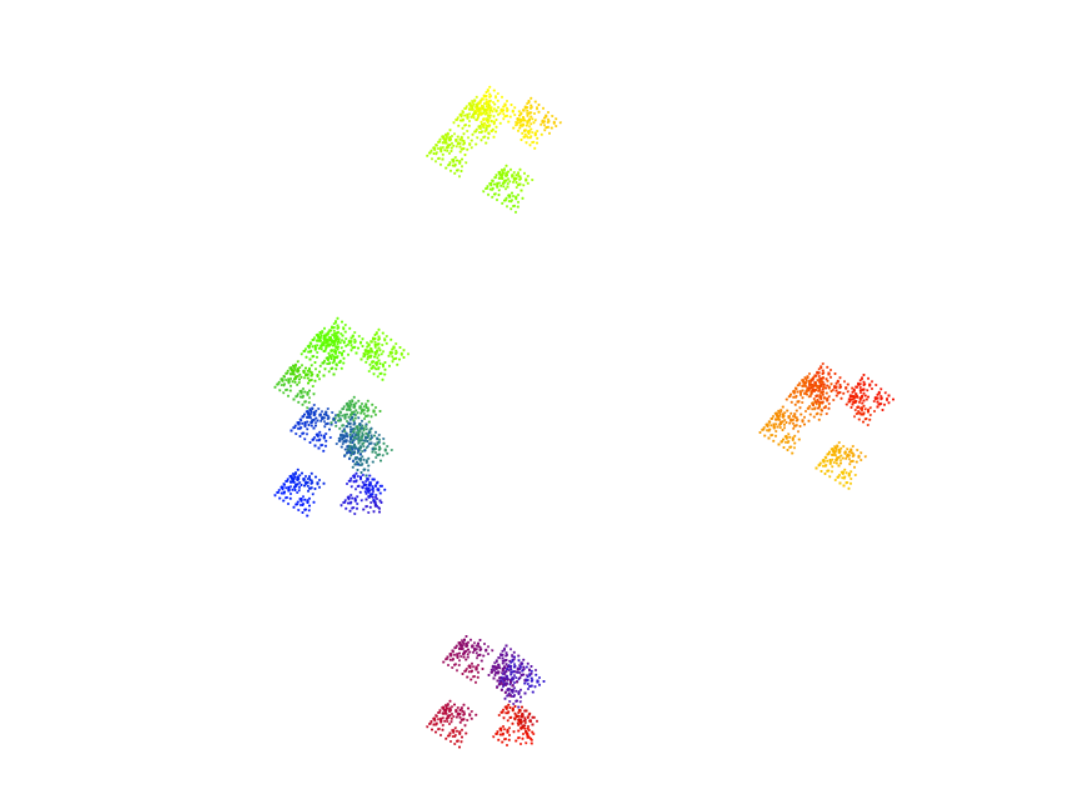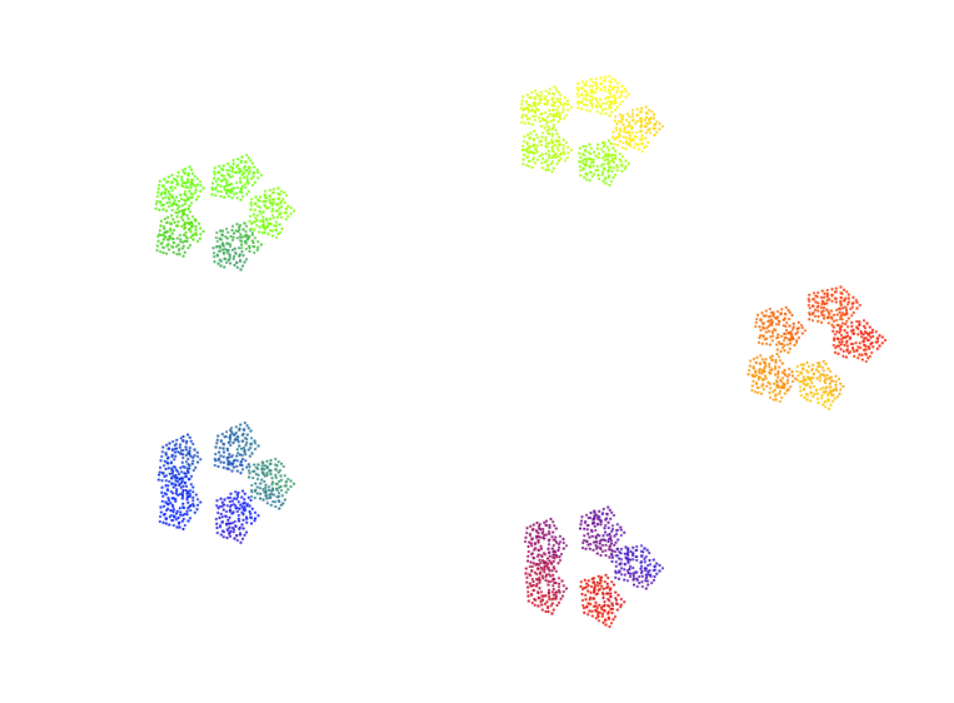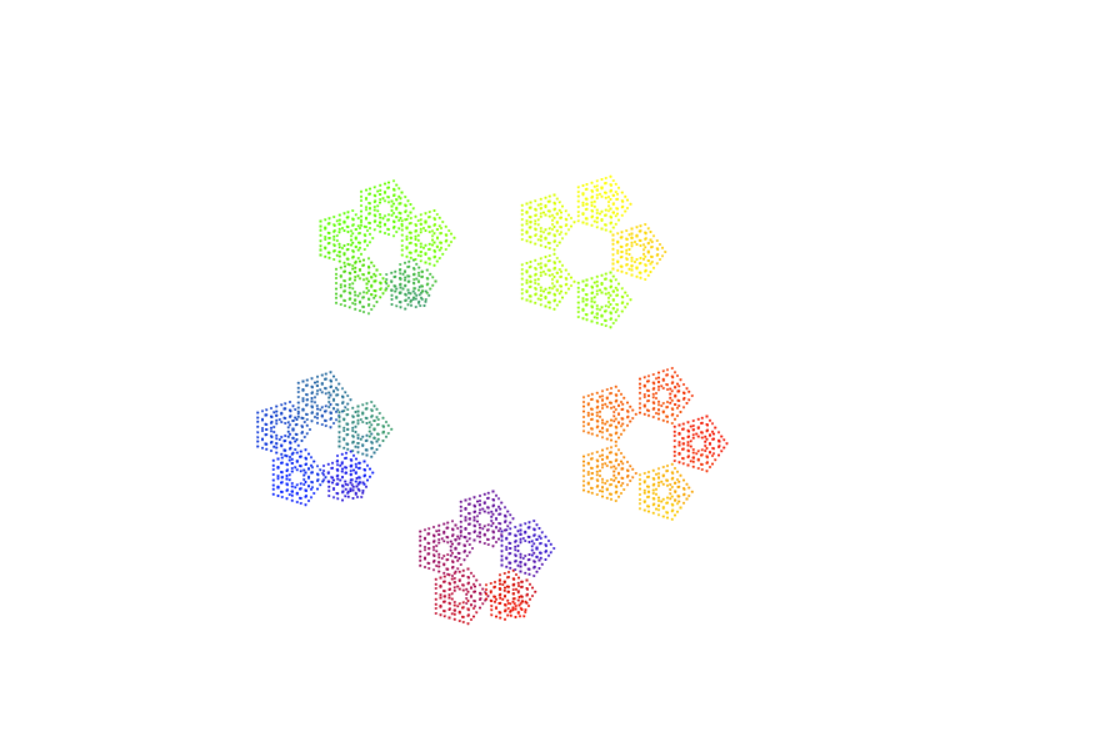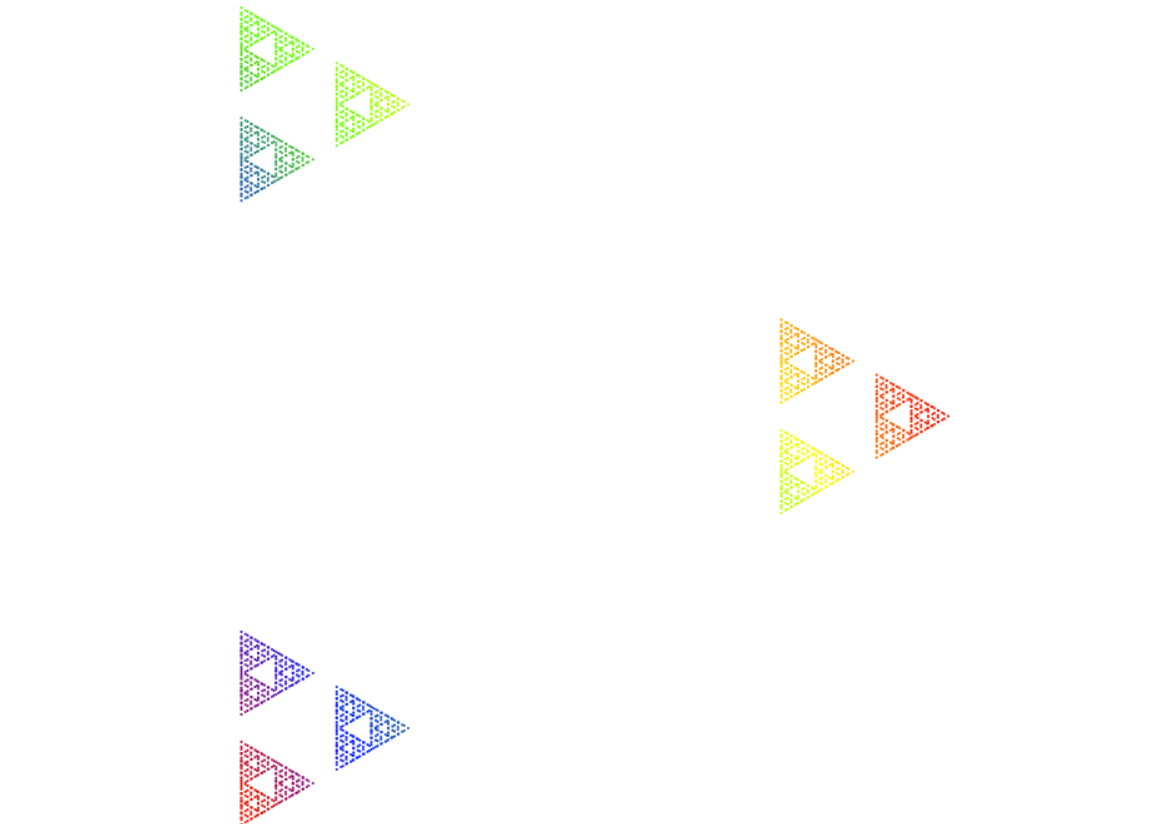Interactive Arithmetic of the p-adic Numbers

The p-adic numbers are a way to use analytic methods (like calculus) to study number theoretic problems (for example, about integers). But wait...calculus only really knows about smallness, and can't tell if something is a whole number or not. To fix this, we endow numbers with something called the p-adic topology, where now smallness=divisibility, that is, things with more factors are smaller (strictly speaking we do this one prime at a time). Now tools like calculus can talk about integers, because those are the smaller things in this topology!
But what does this topology look like? What things are close together? What things are far apart? What about arithmetic. Arithmetic in the real or complex numbers is very geometric, adding is just shifting! So what does arithmetic of p-adic numbers look like geometrically? This question motivated a group of us at ICERM including Katherine Stange and Edmund Harris among others, and it led to this experiment.
Click below to play with two interactive models of the p-adic numbers, which allow you to add, subtract, multiply, and exponentiate (no division yet...), and see what happens to the p-adic number line! The first a circular model, which essentially gives the p-adic topology to Z/pnZ for large n. The second is a (perhaps more accurate) cantor set model, which seems to capture the fractal like nature of the p-adic numbers. I should point out that both are works in progress. If you have any comments or find any bugs please let me know!
Circular Model: Play



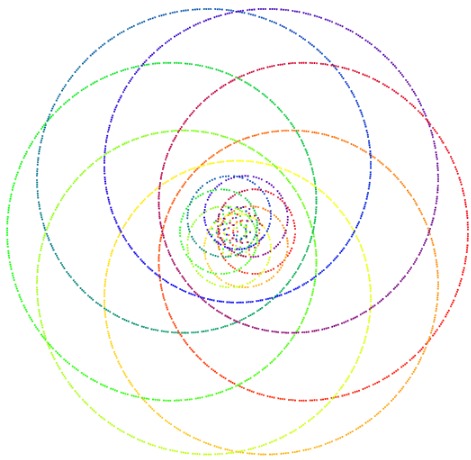
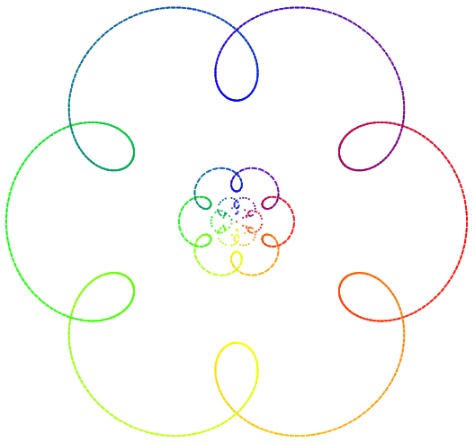
Cantor Set Model: Play